In the last post we used previous day’s minimum and maximum temperatures to forecast tomorrow’s maximum temperature. In this post, we’ll see if we can improve the accuracy of the model using feature engineering. In terms of a benchmark, the Australian Bureau of Meterology published1 a ‘1 day out’ error of ~1.6oC while Holmstrom et al2 report a ‘1 day out’ RMS error of ~2.8oC.
We’ve covered the following code in the previous post so we’ll skip through it here, we’re essentially retrieving files and concatenating them into a dataframe. The code block can be expanded by clicking.
library("readr")
library("dplyr")
library("lubridate")
link_address <- "ftp://ftp.bom.gov.au/anon/gen/clim_data/IDCKWCDEA0.tgz"
download.file(link_address, "data/weather.tgz")
untar("data/weather.tgz", exdir = "data/")
weather_readr <- function(file_name = "file name") {
df_names <- c("Station", "Date", "Etrans", "rain", "Epan", "max_Temp", "min_Temp", "Max_hum", "Min_hum", "Wind", "Rad")
read.csv(text=paste0(head(readLines(file_name), -1), collapse="\n"), skip = 12, col.names = df_names)
}
file_loc <- "data/tables/vic/melbourne_airport/"
df <- data.frame()
for (files in list.files(file_loc, full.names = TRUE, pattern="*.csv")) {
dfday <- weather_readr(files)
df <- rbind(df, dfday)
}
df <- df %>%
mutate(Date = dmy(Date))
Pre-processing
In the last post we manually added previous days minimum and maximum temperatures, this time we’ll just create a function, and use it to add the last 2 days of temperature.
library("dplyr")
calc_prev_temps <- function(df_in, n_days) {
df_in %>%
select(Date, max_Temp, min_Temp) %>%
mutate(TempMax = lag(max_Temp, n = n_days),
TempMin = lag(min_Temp, n = n_days)) %>%
select(TempMax, TempMin)
}
# loop through the last 7 days
df_input <- df
for (i in 1:7) {
df_day <- calc_prev_temps(df_input, i)
df_input <- bind_cols(df_input, df_day)
}
# Exclude non predictor columns
df_input <- df_input %>% select(-c(1:5,7:11))
Let’s take a look at the data now, the left hand column is “today’s maximum”. The remaining columns are previous maximum and minimum temperature.
| max_Temp | TempMax | TempMin | TempMax1 | TempMin1 |
|---|---|---|---|---|
| 29 | 29.2 | 8.1 | 21.1 | 6.3 |
| 31.7 | 29 | 9.7 | 29.2 | 8.1 |
| 21.4 | 31.7 | 13.5 | 29 | 9.7 |
| 18.4 | 21.4 | 15.8 | 31.7 | 13.5 |
| 19.7 | 18.4 | 9.7 | 21.4 | 15.8 |
| 23.6 | 19.7 | 10.2 | 18.4 | 9.7 |
As before we can split the data into a training and test set to build a model and measure it’s accuracy. Last time we used the crude but easily understood Mean Average Error as our accuracy metric, we will report this figure and the Root Mean Squared Error (RMSE) so we may directly compare the results with those of Holmstrom et al.
Modelling
library(h2o) h2o.init() hex_df1 <- as.h2o(df_input) hex_df1 <- h2o.splitFrame(hex_df1) # split into test and training weather_model <- h2o.gbm(training_frame = hex_df[[1]], y = 1) h2o.performance(weather_model, hex_df[[2]]) RMSE: 4.09 MAE: 3.05
This is an improvement over our last model. Let’s see if we can improve it more.
Going further
We can extend the function above to include other weather phenomenon; humidity, wind, rain, radiation and evapotranspiration (me neither).
Pre-processing
calc_prev_phen <- function(df_in, n_days) {
df_in %>%
mutate(TempMax = lag(max_Temp, n = n_days),
TempMin = lag(min_Temp, n = n_days),
Etrans_lag = lag(Etrans, n = n_days),
rain_lag = lag(rain, n = n_days),
Epan_lag = lag(Epan, n = n_days),
Max_hum_lag = lag(Max_hum, n = n_days),
Min_hum_lag = lag(Min_hum, n = n_days),
Wind_nlag = lag(Wind, n = n_days),
Rad_nlag = lag(Rad, n = n_days)
) %>%
select(TempMax, TempMin, Etrans_lag, rain_lag, Epan_lag, Max_hum_lag, Min_hum_lag, Wind_nlag, Rad_nlag)
}
As above, we use the function in a loop to build features for the past seven days for each of the phenomenon.
df_input2 <- df
for (i in 1:7) {
df_day <- calc_prev_phen(df_input2, i)
df_input2 <- bind_cols(df_input2, df_day)
}
df_input2 <- df_input2 %>% select(-c(1:5,7:11))
We can preview the data:
| Date | max_Temp | TempMax | TempMin | Etrans_lag | rain_lag | Epan_lag | Max_hum_lag | Min_hum_lag | Wind_nlag | Rad_nlag | TempMax1 | TempMin1 | Etrans_lag1 | rain_lag1 | Epan_lag1 | Max_hum_lag1 | Min_hum_lag1 | Wind_nlag1 | Rad_nlag1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10/01/2009 | 23.6 | 19.7 | 10.2 | 5.7 | 0 | 5.6 | 79 | 42 | 5.37 | 33.82 | 18.4 | 9.7 | 5.3 | 0.2 | 5.2 | 82 | 35 | 7.03 | 27.48 |
| 11/01/2009 | 23.5 | 23.6 | 10.7 | 5.8 | 0 | 7.2 | 91 | 45 | 4.48 | 32.66 | 19.7 | 10.2 | 5.7 | 0 | 5.6 | 79 | 42 | 5.37 | 33.82 |
| 12/01/2009 | 25.1 | 23.5 | 10.7 | 5.3 | 0 | 6.6 | 90 | 45 | 3.89 | 28.91 | 23.6 | 10.7 | 5.8 | 0 | 7.2 | 91 | 45 | 4.48 | 32.66 |
| 13/01/2009 | 37.1 | 25.1 | 10.4 | 5.4 | 0 | 5.2 | 91 | 43 | 3.55 | 28.02 | 23.5 | 10.7 | 5.3 | 0 | 6.6 | 90 | 45 | 3.89 | 28.91 |
| 14/01/2009 | 33.5 | 37.1 | 11.5 | 11.7 | 0 | 6.8 | 89 | 8 | 6.19 | 34.67 | 25.1 | 10.4 | 5.4 | 0 | 5.2 | 91 | 43 | 3.55 | 28.02 |
Modelling
Our data set is significantly larger now, but will it increase accuracy?
hex_df2 <- as.h2o(df_input2) hex_df2 <- h2o.splitFrame(hex_df2) # split into test and training weather_model2 <- h2o.gbm(training_frame = hex_df2[[1]], y = 1) h2o.performance(weather_model2, hex_df2[[2]]) RMSE: 3.58 MAE: 2.64
We have squeezed out a little more predictive power from our model, however the predictive error is still larger than the RMSE reported in the literature of ~2.8oC.
We can plot the actual values against the predicted:
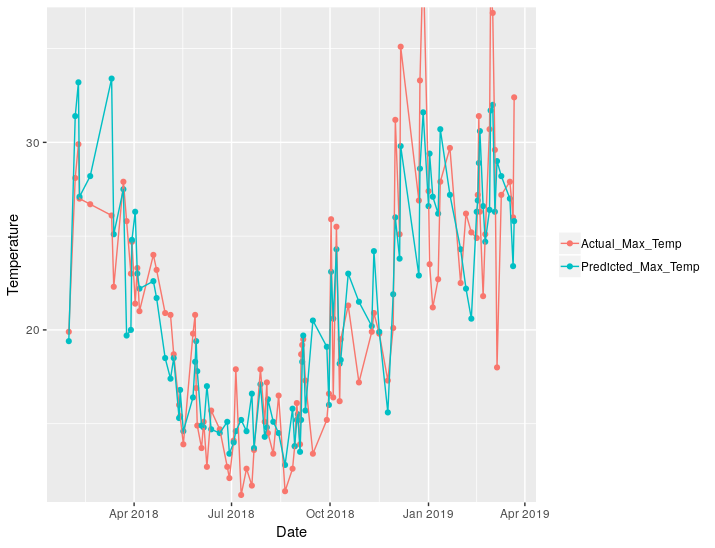
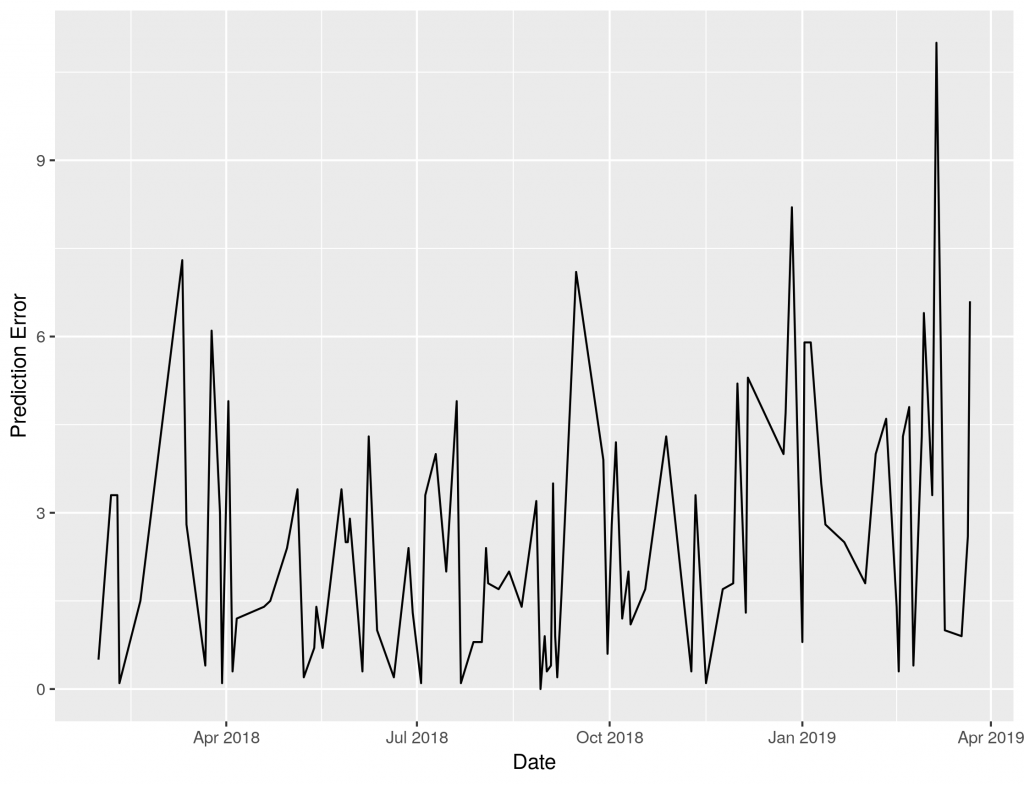
And we can plot just the difference. There is clearly an increase in error in the warmer months, that’s November-March for northern hemispherical readers.
In our next blog, we’ll use one more trick to improve our model.
References
1. Stern, The accuracy of weather forecasts for Melbourne, Australia 2007
2. Holmstrom, Liu, Vo Machine Learning Applied to Weather Forecasting, 2016
